Machine learning for predicting the survival in osteosarcoma patients: Analysis based on American and Hebei Province cohort
DOI:
https://doi.org/10.17305/bb.2023.8804Keywords:
Osteosarcoma, prognosis model, TNM group, Surveillance, Epidemiology, and End Results (SEER), Hebei ProvinceAbstract
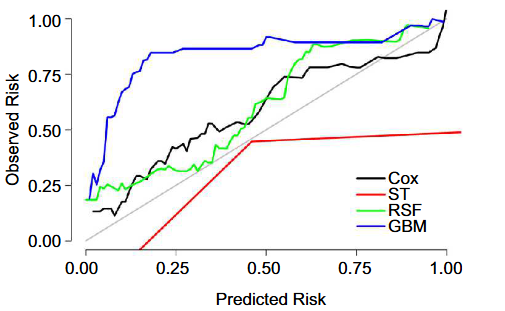
Osteosarcoma, a rare malignant tumor, has a poor prognosis. This study aimed to find the best prognostic model for osteosarcoma. There were 2912 patients included from the SEER database and 225 patients from Hebei Province. Patients from the SEER database (2008-2015) were included in the development dataset. Patients from the SEER database (2004-2007) and Hebei Province cohort were included in the external test datasets. The Cox model and three tree-based machine learning algorithms (survival tree [ST], random survival forest [RSF] and gradient boosting machine [GBM]) were used to develop the prognostic models by 10-fold cross-validation with 200 iterations. Additionally, performance of models in the multivariable group was compared with the TNM group. The 3-year and 5-year cancer specific survival (CSS) were 72.71% and 65.92% in the development dataset, respectively. The predictive ability in the multivariable group was superior to that in the TNM group. The calibration curves and consistency in the multivariable group were superior to those in the TNM group. The Cox and RSF models performed better than the ST and GBM models. A nomogram was constructed to predict the 3-year and 5-year CSS of osteosarcoma patients. The RSF model can be used as a nonparametric alternative to the Cox model. The constructed nomogram based on the Cox model can provide reference for clinicians to formulate specific therapeutic decisions both in America and China.
Citations
Downloads
Downloads
Additional Files
Published
Issue
Section
Categories
License
Copyright (c) 2023 Yahui Hao, Di Liang, Shuo Zhang, Siqi Wu, Daojuan Li, Yingying Wang, Miaomiao Shi, Yutong He

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Accepted 2023-03-23
Published 2023-09-04









